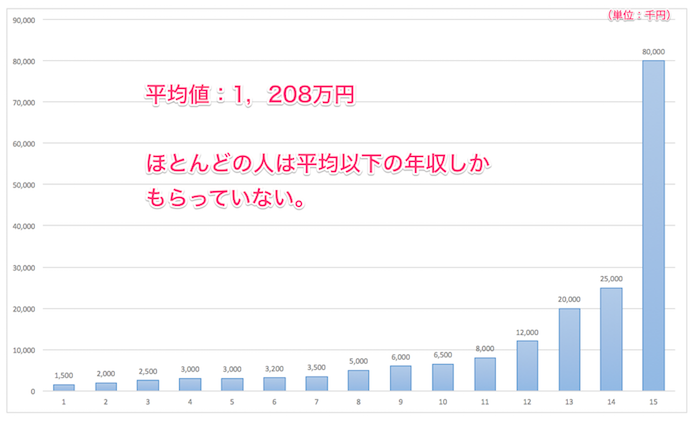
国税庁の調査によれば、日本人の平均年収は414万円だそうだ。（平成25年分 民間給与実態統計調査 国税庁 長官官房 企画課）

読者の実感に合うだろうか？「わたしはそんなにもらってないよ」と思っただろうか？
今回は、平均値のトリックとそれに騙されないための注意点について書く。

通常の平均（算術平均）

皆が通常使っている平均値は、正確には「算術平均」と呼ばれるものだ。
データを全て合計してデータの個数で割り算するだけだ。
学校でも習うし、直感的にも理解しやすい。ちなみにエクセルではAVERAGE関数を使って計算できる。

上記の平均年収（414万）も、算術平均を用いて算出している。
「みんなにそんなもらっているのか・・・」と落ち込む必要はない。
なぜなら「外れ値」が大きな影響を及ぼしているからだ。

年収データの場合、最も低い年収はゼロ円である。
マイナスになるとすれば、お金を払いながら仕事をすることになり、そんな奇特な方はあまりいないと思う。

しかし「最も高い年収」というのは存在しない、お金持ちにはきりがない。
国税庁の調査では年収2,500万円以上の方は11万3千人いるようだ。
このなかには、2,501万円の方もいれば、数億円の方もいるだろう。

極端な例で考えてみよう。
A氏の年収300万、B氏の年収600万。二名の平均年収は450万だ。
この中に、年収3千万のC氏が入るとどうなるか？平均値はいっきに押し上げられて、平均年収1,300万になってしまう。A氏とB氏は「そんなにもらってないけどなあ」と不思議に思うことだろう。
この場合のC氏が「外れ値」だ。
他のデータと大きく違う値が存在すると、算術平均に大きな影響を与える。

上の表では、一人だけずば抜けて年収の高い方（8千万円）がいるために、平均値が押し上げられて多数の方の実感とはずれた値となっている。